Radiative Heat Transfer Between Graphene-Covered Magnetic Weyl Semimetals

Research Background
As a class of promising materials, Weyl Semimetals (WSMs) have garnered considerable attention due to their outstanding optical and electrical properties, which arise from the unique topological features of their Weyl nodes. In particular, magnetic WSMs display strong intrinsic nonreciprocity because of their significant optical gyration. This enables them to break time-reversal symmetry without any external magnetic field, making them highly promising for applications in optical isolators, nonreciprocal thermal emitters, and even chiral modulation and thermal routing in near-field radiative heat transfer (NFRHT) systems. Notably, they also support surface plasmon polaritons (SPPs) known as Weyl SPPs (WSPPs) in the mid-infrared spectrum, exhibiting flexible tunability. These advantages have led to numerous advancements in NFRHT based on magnetic WSMs.
Another well-known plasmonic material is graphene, which is also a typical semimetal. Graphene SPPs (GSPPs) can achieve tunable plasmonic dispersion through chemical doping or gate voltage. By covering a single layer of graphene on other plasmonic materials (e.g., doped silicon), radiative heat flux can be significantly enhanced and actively regulated by coupling SPPs. However, as far as we know, the coupling mechanism between GSPPs and WSPPs in magnetic WSMs remains unclear.
Research Content
In this study, we investigate NFRHT between two graphene-covered Weyl plates with different chemical potentials. We calculate the dispersion relations, demonstrating WSPPs, GSPPs, and coupled SPPs. We also analyze the effects of Weyl node count and Fermi level. Finally, considering the high tunability often present in heterostructures, we propose several typical heterostructures for comparison.
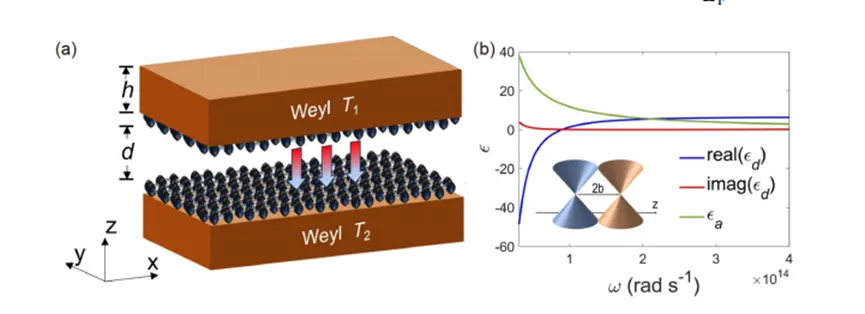
In Figure 1(a), two symmetric graphene-covered magnetic Weyl plates (referred to as G-Weyl) are separated by a real-space gap dd and held at temperatures T1=(T+ΔT)T_1 = (T + \Delta T) and T2=TT_2 = T. For simplicity, we consider a magnetic Weyl plate with an even number of Weyl nodes and a wave vector spacing of 2b2b based on the Nielsen-Ninomiya theorem, and we orient the nodes of the Weyl plates along the zz-axis, i.e., b=bzb = b_z (Figure 1(b)). Therefore, 2b2b resembles an external magnetic field applied to the magneto-optical plate but is entirely due to the intrinsic electronic structure of the magnetic WSM.
Research Findings

- Influence of Chemical Potential (μ) on NFRHT:
We first consider the impact of graphene’s chemical potential μ\mu on NFRHT between two G-Weyl plates (Figure 2(a)). The gap distance d=20d = 20 nm and T=300T = 300 K. For comparison, we also present the total heat transfer coefficient (HTC) of two bare Weyl plates and two single-layer graphene sheets. When μ=0.1\mu = 0.1 eV, the total HTC between the two G-Weyl plates reaches a maximum value of 14×10314 \times 10^3 W m−2^{-2} K−1^{-1}, which is seven times the total HTC between two bare Weyl plates (2.1 \times 10^3 W m−2^{-2} K−1^{-1}). As μ\mu increases, the total HTC monotonically decreases but still exceeds the HTC between two Weyl plates until μ=0.7\mu = 0.7 eV. In other words, depending on the value of μ\mu, adding single-layer graphene sheets can suppress or enhance the heat flux density. For instance, at μ=0.1\mu = 0.1 eV, the total HTC between two single-layer graphene sheets is 23×10323 \times 10^3 W m−2^{-2} K−1^{-1}, which is higher than that of the G-Weyl configuration, but for μ>0.3\mu > 0.3 eV, the HTC drops sharply and becomes smaller. For higher values of μ\mu, the HTC between two Weyl plates surpasses that of the other two configurations; for example, at μ=0.9\mu = 0.9 eV, it is 1.8 and 3.5 times that of the two G-Weyl plates and two single-layer graphene sheets, respectively.
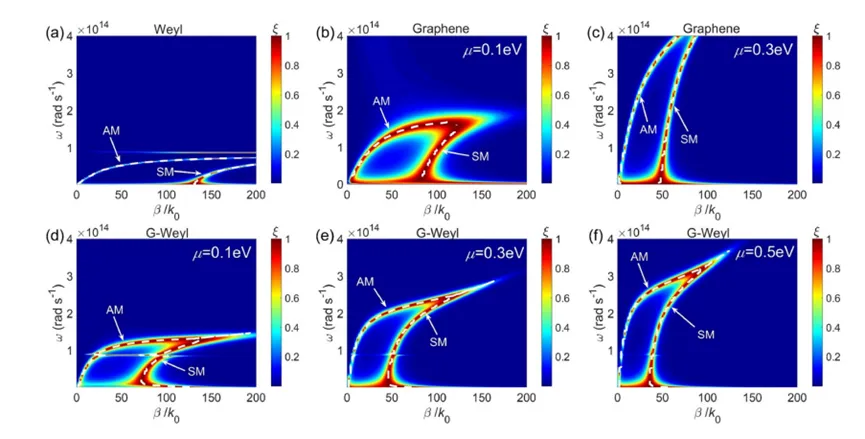
Figure 3 shows the transmission coefficients between (a) two bare Weyl plates, (b) two single-layer graphene sheets at 0.1 eV, and (c) 0.3 eV, and between two G-Weyl plates at (d) 0.1 eV, (e) 0.3 eV, and (f) 0.5 eV. The white dashed lines represent the dispersion relationship of the SPP modes. For the Weyl plates, EF=0.15 eVE_F = 0.15 \, \text{eV} and g=2g = 2.
Generally, WSMs have an even number of Weyl nodes, so the total chirality of all nodes cancels out. Now we consider the effect of the number of Weyl nodes on NFRHT in the G-Weyl configuration. Figure 4(a) compares the total HTC of Weyl plates with and without graphene layers. For bare Weyl plates, the total HTC increases with gg until reaching a maximum of 5.5×103 W m−2 K−15.5 \times 10^3 \, \text{W m}^{-2} \, \text{K}^{-1} at g=16g = 16, which is more than twice the HTC at g=2g = 2. Graphene coverage significantly enhances the total HTC, especially for small values of gg. For instance, the total HTC in the G-Weyl configuration for g=2g = 2 (4) is 13.8×103 W m−2 K−113.8 \times 10^3 \, \text{W m}^{-2} \, \text{K}^{-1} (12.5×103 W m−2 K−112.5 \times 10^3 \, \text{W m}^{-2} \, \text{K}^{-1}), which is 6.5 (3.3) times the HTC of the bare configuration. This is due to the strong coupling SPPs in the G-Weyl configuration, which significantly broadens the spectral peak, making HTC in this configuration more widespread than in the bare configuration (Figure 4(b)). In contrast to the bare configuration, the total HTC of the G-Weyl configuration decreases monotonically with increasing gg, with a decay rate of α=4.4\alpha = 4.4. When g=40g = 40, the total HTCs of both configurations are nearly identical, as their HTC spectra in Figure 4(b) show only a small difference at ω=2.25×1014 rad s−1\omega = 2.25 \times 10^{14} \, \text{rad s}^{-1}.
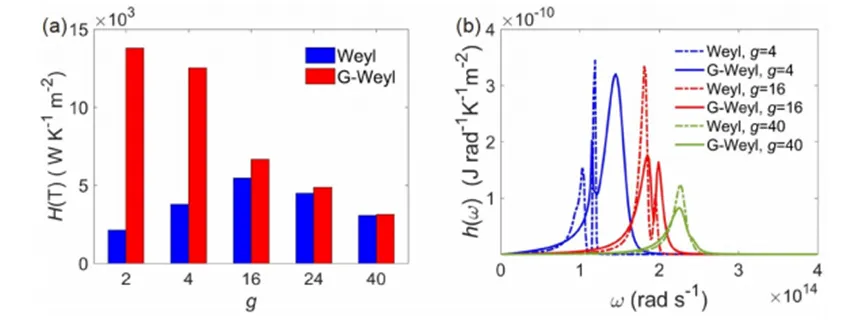
Figure 4 shows (a) the variation of total HTCs of the bare Weyl and G-Weyl configurations with gg and (b) the spectral HTCs for both configurations at g=4g = 4, 1616, and 4040. In the calculations, μ=0.1 eV\mu = 0.1 \, \text{eV} and EF=0.15 eVE_F = 0.15 \, \text{eV}.

Figure 5 shows the transmission coefficients for the bare Weyl (a)-(c) and G-Weyl (d)-(f) configurations at g=4g = 4, 1616, and 4040. In both configurations, the SM and AM branches of SPPs (including WSPPs and coupled SPPs) shift to higher frequencies with increasing gg, while the corresponding parallel wavevector decreases. The ENZ effect, indicated by the horizontal bright lines, weakens and disappears when g=40g = 40, explaining why the HTC spectrum has only one peak. Thus, for the bare Weyl configuration, radiation heat transfer transitions from being dominated by the ENZ effect to being dominated by WSPPs as gg increases. In contrast, the addition of graphene layers to the Weyl configuration produces stronger coupled SPPs over a broader frequency range, especially when g=4g = 4 and 1616. For example, when g=4g = 4, the ENZ branch can pass through the two branches of coupled SPPs. When g=16g = 16, the ENZ and coupled SPPs split, resulting in two comparable peaks in the HTC spectrum. When g=40g = 40, the ENZ branch disappears, similar to the bare configuration. For the G-Weyl configuration, increasing gg suppresses coupled SPPs and ENZ, thereby weakening NFRHT.
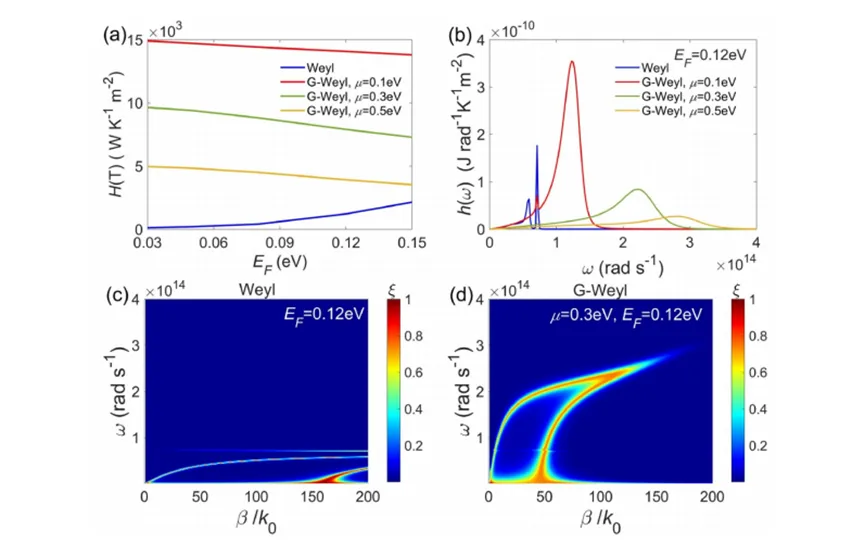
Figure 5 shows the transmission coefficients between (a)-(c) two bare Weyl plates and (d)-(f) two G-Weyl plates at g=4g = 4, 1616, and 4040. In the calculations, μ=0.1 eV\mu = 0.1 \, \text{eV} and EF=0.15 eVE_F = 0.15 \, \text{eV}.
Because the carrier concentration in WSMs is easily depleted, the Fermi energy (EFE_F) depends strongly on temperature. Magnetic WSMs show excellent tunability of the EFS via gate control and thermal tuning, which significantly affects the dielectric constant. To reveal the impact of EFE_F on NFRHT, Figure 6(a) shows the total HTC of the bare and G-Weyl configurations as a function of EFE_F. With increasing EFE_F, the total HTC of the bare Weyl configuration increases, with α=17.8\alpha = 17.8, while the total HTC of the G-Weyl configuration decreases, with much smaller α\alpha values, α=1.1\alpha = 1.1 and 1.41.4 for μ=0.1 eV\mu = 0.1 \, \text{eV} and 0.5 eV0.5 \, \text{eV}, respectively. Taking EF=0.12 eVE_F = 0.12 \, \text{eV} as an example, the corresponding HTC spectrum is plotted in Figure 6(b). Compared to Figure 2(b), the ENZ peak of the Weyl plates redshifts and becomes much lower when EF=0.12 eVE_F = 0.12 \, \text{eV}, reducing the total HTC despite the high β\beta of WSPPs at low frequencies. For instance, at EF=0.12 eVE_F = 0.12 \, \text{eV}, β/k0\beta / k_0 is 155155 near zero frequency, as shown in Figure 6(c). For the G-Weyl configuration, the effect of EFE_F on NFRHT is relatively weak, as shown in the transmission coefficients in Figures 6(d) and 3(e).
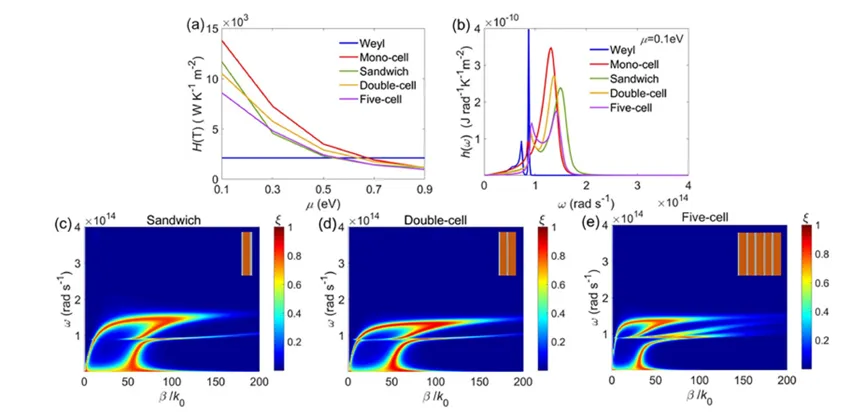
Figure 6 shows (a) the variation of total HTCs of the bare and G-Weyl configurations with EFE_F, (b) the spectral HTCs of the two configurations at EF=0.12 eVE_F = 0.12 \, \text{eV}, and (c)-(d) the transmission coefficients between two Weyl plates (c) and two G-Weyl plates (d) at EF=0.12 eVE_F = 0.12 \, \text{eV}. In the calculations, g=2g = 2 for the Weyl plates.
Heterostructures generally have higher tunability than single-cell structures, achievable by altering layer thickness, filling rate, and so forth. We compared several typical heterostructures, including one, two, and five units of G-Weyl plates (referred to as single-cell, double-cell, and five-cell configurations) and a sandwich structure made of Weyl plates covered with graphene on both sides. Figures 7(a) and 7(b) show that, among these configurations, the single-cell structure has the broadest apparent peak due to the coupled SPPs, leading to the largest total HTC among the other structures.
Figure 7 shows (a) the total heat flux versus μ\mu for bare Weyl, single-cell, sandwich, double-cell, and five-cell structures, and (b) the corresponding spectral heat flux at μ=0.1 eV\mu = 0.1 \, \text{eV}. Figures (c)-(e) show the transmission coefficients for sandwich, double-cell, and five-cell structures (insets) at μ=0.1 eV\mu = 0.1 \, \text{eV}. In the calculations, EF=0.15 eVE_F = 0.15 \, \text{eV} and g=2g = 2 for the Weyl plates.
Conclusion and Outlook
We investigated NFRHT between G-Weyl plates with varying graphene chemical potential, analyzing the effects of Weyl node count gg and Fermi level EFE_F. For bare Weyl plates, NFRHT is dominated by the ENZ effect rather than WSPPs. Adding single-layer graphene sheets creates strong coupled SPPs between GSPPs and WSPPs, suppressing the ENZ effect by compressing the parallel wavevector, which significantly alters HTC. For the G-Weyl configuration, increasing gg suppresses SPP coupling and the ENZ effect, reducing NFRHT with α=4.4\alpha = 4.4. With increasing EFE_F, the total HTC of the G-Weyl configuration slightly decreases with smaller α\alpha values, α=1.1\alpha = 1.1 at μ=0.1 eV\mu = 0.1 \, \text{eV}, while the bare Weyl configuration has α=17.8\alpha = 17.8. Considering that heterostructures generally have higher tunability, we also proposed several typical heterostructures, including double-cell, five-cell structures and sandwich structures. The results show that the single-cell structure has the broadest peak due to the presence of coupled SPPs, resulting in a total HTC that is greater than that of other structures. These findings will contribute to a deeper understanding of the radiation heat transfer associated with surface plasmon coupling and provide opportunities for nanoscale energy harvesting and thermal management based on WSM systems.

